2023년 8월 26일 알고리즘 문제풀이
문제 1 프로그래머스 전력망을 둘로 나누기
1차 시도
나의 생각
한 간선이 없어질 때마다 값을 모두 구한 후 가장 절대값이 작을 때를 찾았다.
결과
정답
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from collections import deque
def solution(n, wires):
answer = n
d = len(wires)
for i in range(d):
arr = deque()
arr.append(0)
graph = [[] for _ in range(n)]
visited = [False for _ in range(n)]
visited[0] = True
for j in range(d):
if j == i:
continue
else:
a,b = wires[j]
graph[a-1].append(b-1)
graph[b-1].append(a-1)
while arr:
now = arr.popleft()
for x in graph[now]:
if not visited[x]:
visited[x] = True
arr.append(x)
cnt = visited.count(True)
cnt = abs(n-2*cnt)
answer = min(answer,cnt)
return answer
문제 2 프로그래머스 쿼드압축 후 개수 세기
1차 시도
나의 생각
사각형의 왼쪽 상단 모서리를 기준으로 내용의 정수가 모두 같은지 확인한다. 같지 않을 시 4개로 쪼갠다. 이를 반복하는 함수는 왼쪽 상단 모서리의 좌표와 사각형의 한 변의 길이를 parameter로 받는다.
결과
정답
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def solution(arr):
answer = [0,0]
def change(a,b,n):
if n == 1:
idx = arr[a][b]
answer[idx] += 1
return
else:
val = arr[a][b]
for i in range(a,a+n):
for j in range(b,b+n):
if arr[i][j] != val:
x1,y1 = a,b
x2,y2 = a+n//2,b+0
x3,y3 = a+0,b+n//2
x4,y4 = a+n//2,b+n//2
change(x1,y2,n//2)
change(x2,y2,n//2)
change(x3,y3,n//2)
change(x4,y4,n//2)
return
idx = val
answer[idx] += 1
return
change(0,0,len(arr))
return answer
문제 3 합승 택시 요금
1차 시도
나의 생각
우선 다익스트라 알고리즘을 통해 두 지점 간의 최소 비용을 구하는 함수를 정의한다. 이후 공통된 출발점을 순회하며 각 경우를 계산하고 가장 낮은 값일때를 업데이트한다.
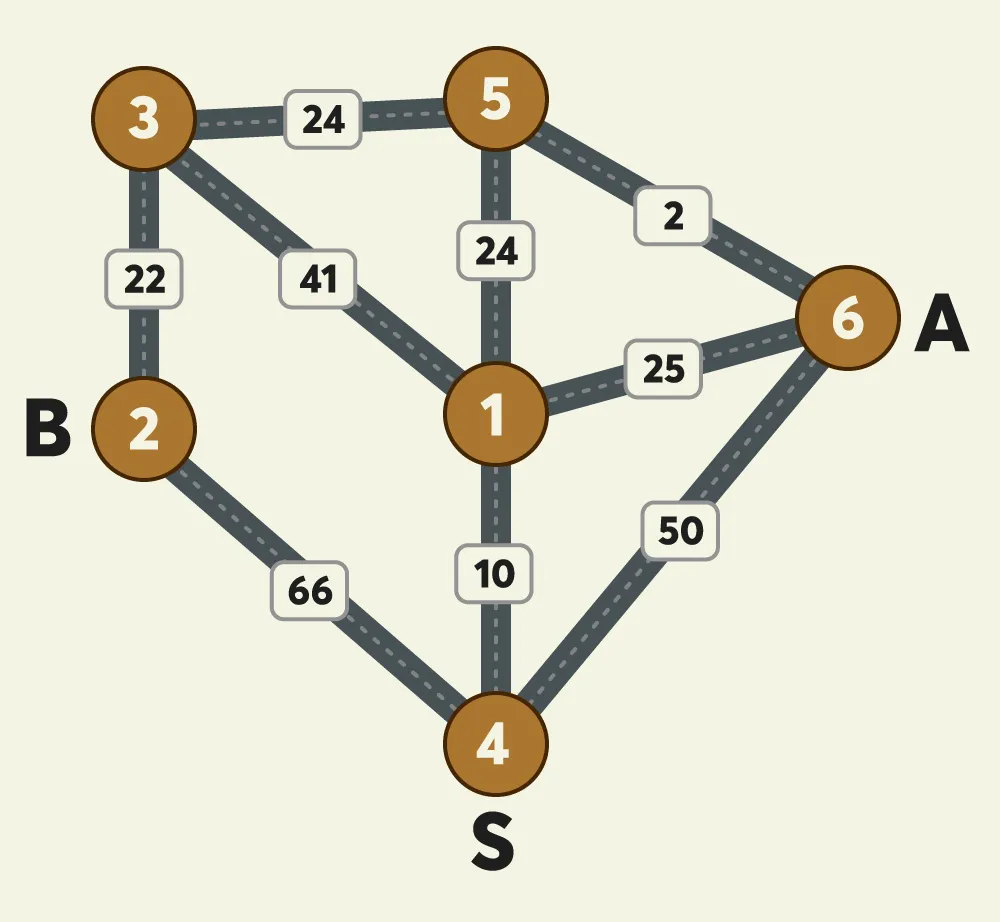
예를 들어, 위 경우를 보자. 기존의 출발지인 4에서 각각 A,B가 집까지 가는 비용을 계산 후 더한다.
그다음은 1에서 각자가 집으로 향하는 비용을 더한 후, 원래 출발지인 4에서 1까지 가는 비용을 더해준다. 그다음은 5에서, 6, 3, 2 에서 출발할 때를 모두 확인한 후 가장 최솟값을 도출하면 된다.
만약 1까지 같이 합승하고 1에서 출발하는 경우를 계산할 때, 둘다 5를 거쳐서 각자의 집으로 가는 경우가 있다면? 그때와 5에서 같이 출발할 떄의 중복은 어떻게 고려해야할까?
이 때는 4에서 1까지 같이 갈때만 합승으로 비용이 절약되고, 두 사람이 1에서 5로 이동하는 비용은 두번 더해진다. 합승으로 처리되지 않기 때문이다. 하지만 5에서 같이 출발하는 경우를 계산할 땐 합승으로 처리되어 한번만 더해진다. 즉 전자는 무조건 후자보다 높은 비용이 나오기 때문에 결과가 달라질 일이 없다!
결과
정확성 50.0
효율성 35.0
85/100
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from collections import deque
def solution(n, s, a, b, fares):
graph = [[0 for _ in range(n+1)] for _ in range(n+1)]
for way in fares:
c,d,f = way
graph[c][d] = f
graph[d][c] = f
def search(start,end):
if start == end:
return 0
visited = [0 for _ in range(n+1)]
arr = deque()
arr.append(start)
while arr:
now = arr.popleft()
for next in range(1,n+1):
if next == now:
continue
if graph[now][next]:
if not visited[next] or visited[next] > visited[now] + graph[now][next]:
visited[next] = visited[now] + graph[now][next]
arr.append(next)
else:
continue
if visited[end]:
return visited[end]
else:
False
answer = search(s,a)+search(s,b)
for i in range(1,n+1):
if s == i or not search(s,i):
continue
tmp = search(s,i) + search(i,a) + search(i,b)
answer = min(tmp,answer)
return answer
2차 시도
나의 생각
로직은 맞았지만 수행시간에 문제가 있었다. 다익스트라이기 떄문에 deuqe을 최소 힙을 사용하여 수행시간을 개선했다.
결과
정답
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from heapq import heappop, heappush
def solution(n, s, a, b, fares):
graph = [[] for _ in range(n+1)]
answer = 1e9
for way in fares:
c,d,f = way
graph[c].append([d,f])
graph[d].append([c,f])
def search(start,end):
visited = [1e9 for _ in range(n+1)]
arr = []
heappush(arr,[0,start])
visited[start] = 0
while arr:
cnt,now = heappop(arr)
if visited[now] < cnt:
continue
for x in graph[now]:
tmp_now, tmp_cnt = x[0], x[1]
tmp_cnt += cnt
if tmp_cnt < visited[x[0]]:
visited[tmp_now] = tmp_cnt
heappush(arr,[tmp_cnt,tmp_now])
return visited[end]
for i in range(1,n+1):
answer = min(answer,search(s,i)+search(i,a)+search(i,b))
return answer