2024년 1월 1일 알고리즘 문제풀이
문제
난이도
Lv.2
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from heapq import heappop, heappush
def solution(A,B):
n = len(A)
arr_A = [False for _ in range(n)]
arr_B = [False for _ in range(n)]
arr = []
def dfs(tmp,arr_A,arr_B):
if arr and tmp > arr[0]:
return
if not arr_A.count(False) and not arr_B.count(False):
if not arr or tmp < arr[0]:
heappush(arr,tmp)
for i in range(n):
if arr_A[i]:
continue
for j in range(n):
if arr_B[j]:
continue
arr_A[i] = True
arr_B[j] = True
dfs(tmp+(A[i]*B[j]),arr_A,arr_B)
arr_A[i] = False
arr_B[j] = False
dfs(0,arr_A,arr_B)
return arr[0]
처음엔 DFS로 시도했다. 여러 case가 규칙성 없이 나타날 수 있다고 생각했기 때문이다. 하지만 시간초과가 발생했다. 불필요한 탐색을 줄이기 위해, 값을 최소힙에 저장하도록 했다. DFS 과정 상 재귀 중에 이미 최소힙에 존재하는 최솟값을 넘어선 경우 탐색을 중단하도록 했다. 하지만 시간초과가 계속 발생했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from heapq import heappop, heappush
def solution(A,B):
answer = 0
n = len(A)
heap_A = []
heap_B = []
for i in range(n):
heappush(heap_A,A[i])
heappush(heap_B,-1*B[i])
for i in range(n):
a = heappop(heap_A)
b = heappop(heap_B)
answer += a*b*(-1)
return answer
문제에서 주어진 예시를 살펴보다가, 양쪽의 최솟값과 최댓값을 순차적으로 곱해서 더하는 값이 답이지 않을까 생각했다. 처음에는 가장 큰 값과 가장 작은 값, 그 다음 두번째로 큰 값과 두번째로 작은 값을 곱하여 더해주는 방식. 매번 탐색하기엔 너무 복잡할 것 같아 배열을 최소힙으로 변경했다. 나머지 하나는 최댓값을 찾아야 하기 때문에 음수로 변형하여 최소힙을 설정해주었다.
결국 답은 구했는데 왜 이게 답인지 모르겠다. 저 코드가 이해가 안되는 건 아닌데, 왜 저때가 최솟값이지? 찾아보니 재배열 부등식의 개념이라고 한다. 교과과정에는 안나오고 경시대회 수학에서 나오는 개념이라는데.. 궁금하니 조금 알아봤다.
재배열 부등식

출처 : 나무위키
위 내용인데, 그리디 알고리즘의 예시 중 하나이다. 쉽게 말하면, 정렬된 두 수열의 원소의 곱의 합은 두 수열이 반대 방향으로 정렬되어 있을 때 가장 작고, 같은 방향으로 정렬되어 있을 때 가장 크다는 내용이다.
다음은 증명이다. 글씨는 양해 바람.
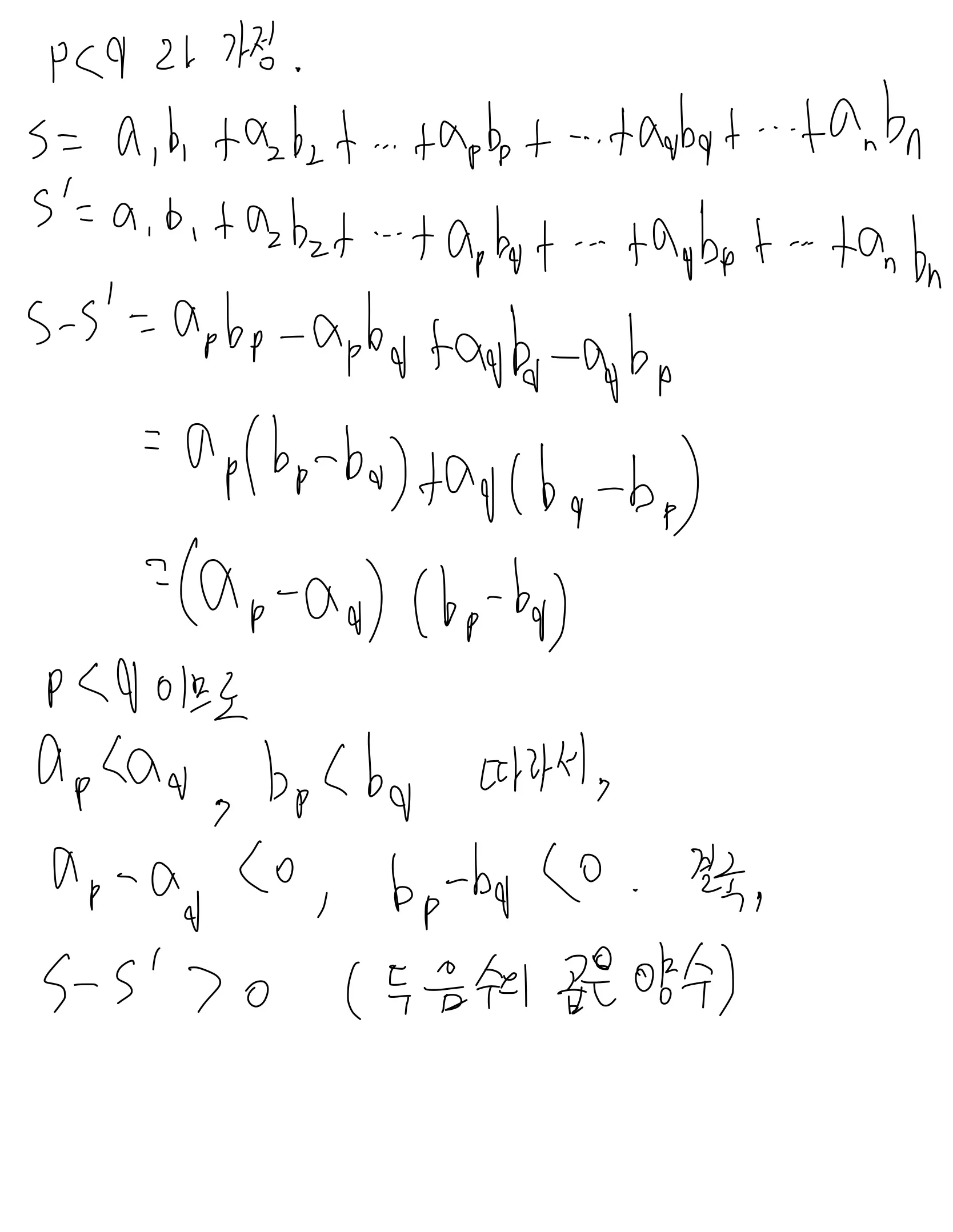
위 증명으로 얻을 수 있는 결론은, 오름차순 정렬되어 있는 두 수열에서 임의의 순서 변화가 발생할 경우 값은 무조건 작아진다는 의미이다. 바꿔 말하면, 두 수열이 똑같이 정렬되어 있을때 가장 큰 값을 가진다는 것.
우리의 경우는 최댓값이 아닌 최솟값이 필요한데, 두 수열을 같은 방향으로 정렬이 아닌 반대 방향으로 정렬하면 결과를 얻을 수 있다. 아래 참고.

위와 같이, 두 수열이 정 반대로 정렬되어 있을때 임의의 순서의 변화가 발생한다면 값은 무조건 커진다는 의미이다.
이제 왜 DFS나 BFS로 모든 경우를 탐색할 필요가 없는지 이해됐다.