4.분할정복
4.2 행렬곱셈을 위한 스트라센 알고리즘
행렬의 곱셈은 다음과 같다
n = A.rows
C는 새로운 n x n 행렬이라 하자.
for i - 1 to n
for j = 1 to n
c_ij = 0
for k = 1 to n
c_ij = c_ij + (a_ik)(b_kj)
return C
3중 반복문이기 때문에 수행시간 Θ(n^3)이다. Ω(n^3)이라고 예상하지만 사실 o(n^3) 방법이 있따.
스트라센 알고리즘(Streassen Algorithm)은 Θ(n^log_2(7))이 소요된다. 2.80 < log_2(7) < 2.81이므로 O(n^2.81) 이라고 할 수 있다.
단순한 분할정복 알고리즘
n = A.rows
C는 n x n 행렬이라 하자.
if n == 1
c_11 = a_11 x b_11
else A, B, C를 다음과 같이 나눈다.
C_11 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_11,B_11)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_12,B_21)
C_12 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_11,B_12)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_12,B_22)
C_21 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_21,B_11)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_22,B_21)
C_22 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_21,B_12)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_22,B_22)
return C
위 코드는 행렬의 곱셈을 분항정복으로 나눠서 생각해본 것이다. 각 원소가 2의 거듭제곱 형태라고 가정하여 계산을 용이하게 한다.
n x n 크기의 행렬을 n/2 x n/2 크기의 행렬 4개로 나누는 것이 원리이다. A 는 A_11, A_12, A_21, A_22 로 나눠진다. B, C도 마찬가지이다. SQUARE-MATRIX-MULTIPLY-RECURSIVE는 행렬에서 곱셈을 나타내는 재귀함수이다. 2X2 크기의 행렬에서
C의 1행 1열 = (A의 1행 1열) x (B의 1행 1열) + (A의 1행 2열) x (B의 2행 1열) 이다. 이걸 나타낸 코드가 위에서 6~7행이다. 재귀인 이유는 저 A_11이 숫자가 아닐 수도 있기 때문이다. n/2 x n/2 크기의 행렬일 수도 있다. 그렇다면 또 그 행렬 내부로 재귀가 호출되어야 계산을 해야한다.
- 분할 : 행렬 C가 행렬 A와 B의 곱이라고 하자. 각각이 n x n 크기의 행렬이라하면 n/2 x n/2 크기의 행렬이 한 개당 4개가 생성되어 총 12개의 행렬이 생성된다. 행렬을 나누는 것의 수행 시간은 어떻게 될까? 행과 열에 따라 복사하려면 Θ(n^2)의 시간이 걸릴 것이다. 하지만 기존 행렬에서 복사하지 않고 범위를 통해서만 부분행렬을 정의하면 Θ(1)이라는 상수의 수행시간으로 만들 수 있다. 왜냐하면, 위에서 나타난대로, 행렬의 곱셈에서 각 원소는 원소간의 곱의 합으로 나타내게 된다. 위에서 설명했듯 이 원소도 행렬이라고 볼 수 있다.
우리가 2x2크기의 행렬을 곱할때 하나의 숫자끼리 곱해져서 더해지지만 이를 1x1 크기의 행렬이라고 볼 수 있는것!
- 계산 : n x n 크기의 행렬간의 곱에 걸리는 수행 시간을 T(n)이라 하자. 그렇다면 n/2 x n/2 크기로 나누었을 때 곱셈의 수행시간은 T(n/2)이다. 이 호출은 8번이 필요하다. n x n 크기의 행렬을 4등분 했으므로, 각각 한 부분의 값을 구할때는 두 행렬의 곱으로 이루어진 두개의 값을 더하기 때문이다. 한 개 당 2개를 더해서 이뤄지니 전체 4개에는 8번의 행렬의 곱셈 과정이 필요하다. 따라서 전체 수행시간은 8T(n/2)이다.
- 조합 : 위에서 8번을 행렬의 곱셈 과정이 8번이 있어야 한다고 했고, 그 결과들을 더하는 데는 얼마나 걸릴까? n/2 x n/2 크기의 행렬에는 (n^2)/4 개의 원소가 있으니, 이는 곧 한 행렬마다 더할 때 걸리는 시간이다. 원소는 4등분을 해서 4개가 나타났으니 4를 곱하면 n^2이다. 따라서 조합에 걸리는 시간은 Θ(n^2)이다.
결국 T(n) = Θ(1) + 8T(n/2) + Θ(n^2) = 8T(n/2) + Θ(n^2)이다. 결론부터 말하자면 이것의 해는 T(n) = Θ(n^3)이다. 자세한 이유는 후에 마스터 방법에서 배우니 결과만 보자. 즉, 분할정복 접근법은 기존의 일반적인 방법보다 빠르지 않다. 이유가 뭘까?
분할에서 행렬을 나눌 때, 나눠야 할 행렬은 A와 B 두개이다. 따라서 하나가 Θ(1) 이니 2를 곱해야 한다. 하지만 Θ-표기법에 의해 상수 2를 생략한 것이다. 조합에서도 Θ((n^2)/4)였지만 Θ-표기법을 근거로 계수 1/4를 생략하였다.
하지만 8T(n/2)에서 8은 생략하지 않았다. 할 수 없다. 8을 생략해서 T(n/2)시간이 걸린다고 말하면 안되고 8T(n/2)라고 해야한다. 이전 2단원에서 병합정렬을 분할정복을 통하여 이해할 때 T(n) = 2T(n/2) + Θ(n) 임을 공부하였다. 이 과정에서 재귀를 보여주는 트리 모양의 형태를 그리면서 각 단계에서 하나하나가 어떤 수행시간을 가지며 그것이 총 몇개있는지 파악하였다. 여기서 2 라는 숫자는 재귀 과정에서 깊숙해 질수록 다음 단계가 몇개의 자식을 가지는 지, 그 깊이에서 몇개를 더해야 하는지에 관여하였다. 결론은
점근적 표기법이 상수 계수를 생략할 수 있다 해도 T(n/2)와 같이 재귀적인 표기에 대해서는 그렇지 않다.
스트라센의 방법
위에 T(n) = 2T(n/2) + Θ(n)에서 T(n/2)의 계수 2를 생략한다면? T(n) = T(n/2) + Θ(n)의 형태가 되고 재귀트리는 점차 갯수가 늘어나는 트리형태가 아니게 되고, 갯수가 유지되는 일직선의 형태를 보일 것이다.
스트라센의 방법은 재귀갯수를 줄이고, 덧셈의 횟수를 늘리는 것이다. 재귀는 생략할 수 없는 계수고, 덧셈은 생략 가능하기 떄문.
스트라센의 방법은 4단계로 이루어진다.
- 크기가 n x n 인 행렬 A와 B, C를 n/2 x n/2를 크기로 하는 부분 행렬들로 나눈다. 상술하였듯 이 과정은 Θ(1)의 시간이 걸린다.
- 행렬을 10개 만들고 각각 S_1, S_2, …, S_10 이라고 하자. 크기는 n/2 x n/2이며 1단계에서 만든 행렬의 합이거나 차이를 의미한다. 행렬 10개를 만드는데 걸리는 시간은 Θ(n^2)일 것이다. 각 행렬의 원소 갯수는 (n^2)/4개인데 10개므로 10을 곱하지만, Θ-표기법이라 계수가 생략되기 때문이다.
- 1단계에서 만든 부분행렬과 2단계에서 만든 10개의 S 행렬을 이용하여 n/2 x n/2 크기의 행렬을 7개 만든다. 각각 P_1, P_2, …, P_7이라고 하자.
- P 행렬들의 다양한 조합을 더하거나 빼서, 원래의 목표였던 행렬 C의 부분 행렬 C_11,C_12,C_21, C_22 를 계산한다. 이 계산은 Θ(n^2)시간이 걸린다.
이걸 토대로 점화식을 세워보자.
T(n) = 7T(n/2) + Θ(n^2)
마스터 정리에 의하면 위 식의 해는 T(n) = Θ(n^(log_2(7))) 이다. 기존의 Θ(n^3) 보다 빠르다. 이유를 세부적으로 살펴보자.
2단계
2단계에서 만든 행렬 S는 다음과 같이 쓸 수 있다.
S_1 = B_12 - B_22
S_2 = A_11 + A_12
S_3 = A_21 + A_22
S_4 = B_21 - B_11
S_5 = A_11 + A_22
S_6 = B_11 + B_22
S_7 = A_12 - A_22
S_8 = B_21 + B_22
S_9 = A_11 - A_21
S_10 = B_11 + B_12
각각은 n/2 x n/2 크기이므로 하나의 원소의 갯수는 (n^2)/4 이다. 10개니까 10을 곱하지만 Θ-표기법에 의해 계수는 생략되므로 Θ(n^2)이다.
3단계
1,2 단계에서 만들어진 행렬들의 재귀 곱으로 7개의 P 행렬을 만든다. 다음과 같이도 만든다.
P_1 = A_11 x S_1 = (A_11 x B_12 ) - (A_11 x B_22)
P_2 = B_22 x S_2 = (A_11 x B_22 ) + (A_12 x B_22)
P_3 = B_11 x S_3 = (A_21 x B_11 ) + (A_22 x B_11)
P_4 = A_22 x S_4 = (A_22 x B_21 ) - (A_22 x B_11)
P_5 = S_6 x S_5 = (A_11 x B_11 ) + (A_11 x B_22) + (A_22 x B_11) + (A_22 x B_22)
P_6 = S_8 x S_7 = (A_11 x B_12 ) + (A_11 x B_22) - (A_22 x B_21) - (A_22 x B_22)
P_7 = S_10 x S_9 = (A_11 x B_12 ) + (A_11 x B_22) - (A_21 x B_11) - (A_21 x B_12)
4단계
이렇게 만든 P 행렬을 더하거나 뺴서 조합하여 행렬 곱 C를 n/2 x n/2 크기의 부분행렬 4개를 만들 것이다.
C_11 = P_5 + P_4 - P_2 + P_6 ( 여기 식에서 P를 위의 값을 넣어 전개하여 정리한다.)
= (A_11 x B_11) + (A_12 x B_21)
C_12, C_21, C_22도 같은 논리를 적용할 수 있다.
각 행렬은 n/2 x n/2 크기이므로 행렬마다 원소 (n^2)/4 개를 가지니 이걸 8번 더하거나 빼므로 이 단계의 수행시간은 Θ(n^2)이다.
위 과정에서 우리는 8번의 재귀가 아닌 7번의 재귀를 호출하였다. 이 과정으로 우리가 알아낸 것은 스트라센 알고리즘이
T(n) = 7T(n/2) + Θ(n^2)
이라는 점화식으로 표현될 수 있다는 것이다. 여기서 어떻게 log_2(7) 값에 도달하게 되는지는 이후 장에서 나온다고 한다.
연습문제
4.2-1
스트라센 알고리즘을 이용해 다음 행렬 곱을 계산하는 과정을 보여라
(1 3) (6 8)
(7 5) (4 2)
나의 답

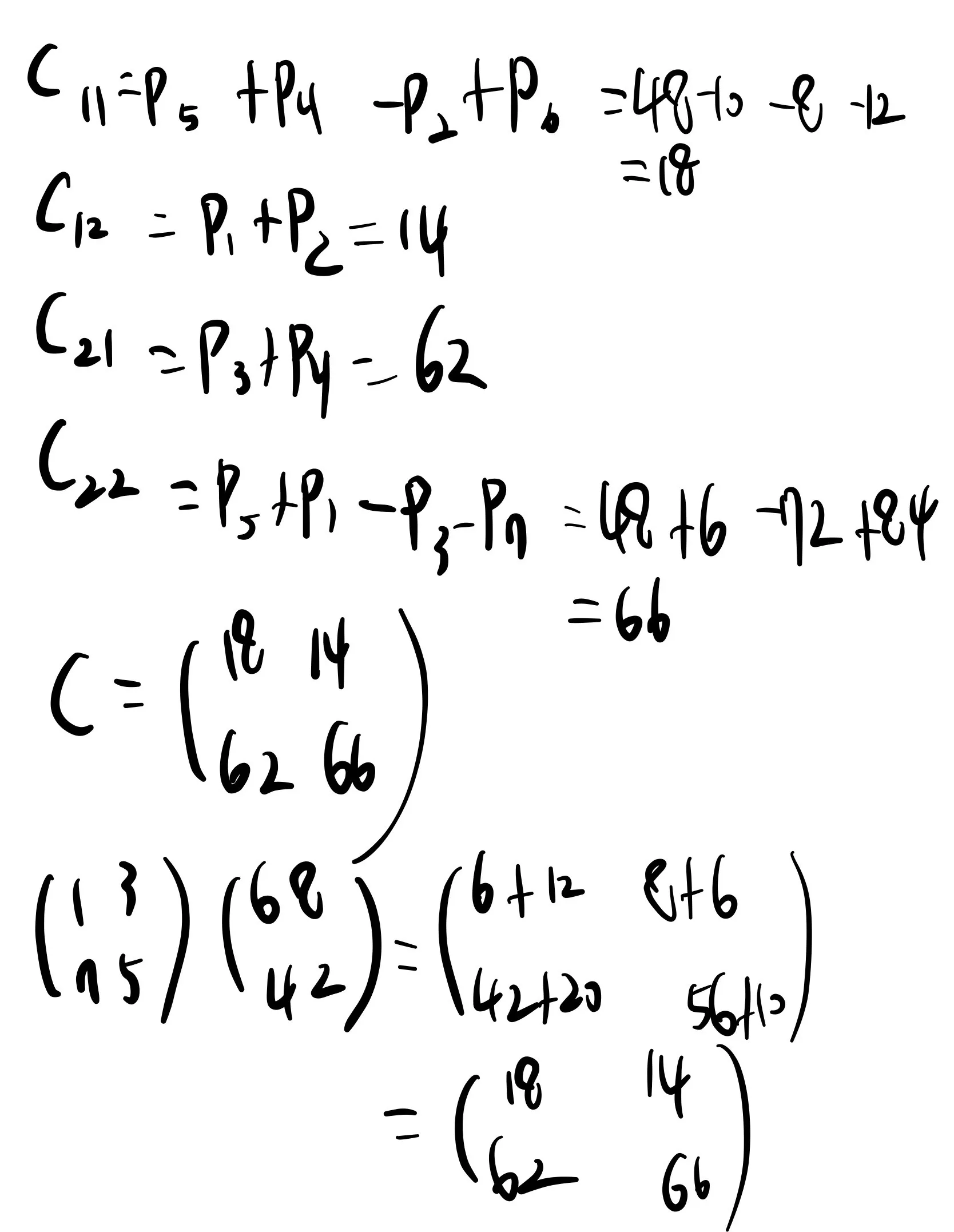
4.2-2
스트라센 알고리즘의 의사코드를 작성하라
나의 답
n = A.rows
C는 n x n 행렬이라 하자.
if n == 1
c_11 = a_11 x b_11
else 행렬 A, B, C 를 각각 n/2 x n/2 크기의 부분행렬 4개로 나눈다.
S1 = A11 + A22
S2 = B11 + B22
S3 = A21 + A22
S4 = B12 - B22
S5 = B21 - B11
S6 = A11 + A12
S7 = A21 - A11
S8 = B11 + B12
S9 = A12 - A22
S10 = B21 + B22
P1 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(S1, S2)
P2 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(S3, B11)
P3 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11, S4)
P4 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22, S5)
P5 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(S6, B22)
P6 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(S7, S8)
P7 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(S9, S10)
C11 = P1 + P4 - P5 + P7
C12 = P3 + P5
C21 = P2 + P4
C22 = P1 - P2 + P3 + P6
return C
4.2-6
스트라센 알고리즘을 서브 루틴으로 사용했을 때 kn x n 행렬과 n x kn 행렬의 곱셈을 얼마나 빨리 계산할 수 있는가? 입력 행렬의 순서를 바꾸었을 때 같은 질문에 답하라.
나의 답
행렬 A가 l x m 크기이고 행렬 B가 m x n 크기일 때, 일반적인 행렬 곱셈은 대략 2lmn번의 연산이 필요함 따라서 문제의 상황에서는 2(k^2) x n^3 번의 연산이 필요하다. 비정방행렬이지만 적용할수는 있되, k , n의 값에 따라 크게 좌우된다. 짝수화를 위해 얼마나 추가적인 과정이 필요한지, 2의 거듭제곱형태로 되기 위해 어느정도 추가 작업이 필요한지, 차원을 감소시켜 일반적인 행렬의 곱셈을 도입하는데 까지 얼마나 필요한지 등이 고려되야 한다. 하지만 입력의 순서를 바꾸었을 땐 연산의 횟수와 결과의 차원이 변하진 않으므로 기존 문제와 차이는 없다고 생각한다.